Obecné otázky o kosmonautice

[Alchymista]

No jednoduchou - teziste je bod, kde se vyrovnavaji vsechny gravitacni sily a jsou nulove.
Barycentrum je teziste soustavy.

Takže toto je jasné...
Zamieňaš si ťažisko objektu v gravitačnom poli, napríklad činku s nerovnakými guľami v gravitačnom poli Zeme, s ťažiskom v systéme dvoch nerovnako hmotných telies viazaných vlastnou gravitáciou. Je to síce ťažisko ako ťažisko, ale v prvom prípade pôsobí na obe telesá rovnaká gravitačná sila tretieho telesa (Zeme), to však nie je sila, ktorou na seba pôsobia tieto dve telesá navzájom.

Máme takýko systém v ktorom je m₁>m₂:
m₁_____T______________m₂
|----r₁---|----------r₂---------|

Pozícia ťažiska je určená "rovnováhou na páke":
m₁.r₁ = m₂. r₂
kde r je dĺžka páky a r₁ a r₂ sú vzdialenosti závaží m₁ a m₂ od ťažiska.

Ale pre intenzitu gravitačného poľa objektu o hmotnosti m vo vzdialenosti R od jeho stredu platí:
E = (G.m) / r²
Kde G je gravitačná konštanta, m hmotnosť objektu a r vzdialenosť od stredu

Pre intenzity gravitačného poľa oboch telies v ťažisku potom platí
E₁ = (G.m₁) / r₁²
E₂ = (G.m₂) / r₂²

a pre rovnosť E₁=E₂ je potrebné hľadať iné vzdialenosti, označme ich l₁, l₂ - tak, aby platilo:
(G.m₁) / l₁² = (G.m₂) / l₂²
pokiaľ má zároveň platiť aj
r = l₁ + l₂
dostane rovnica tvar
(G.m₁) / (r - l₂)² = (G.m₂) / (r - l₁)²
a riešením je vzdialenosť libračného bodu L1 od oboch telies, čo bude v grafickej podobe vyzerať asi takto:
m₁_____T____________L1__m₂
|----r₁---|-----------r₂---------|
|------------l₁--------------|-l₂-|

[MartinH]

...

Tak tohle je přesně tak jak jsem to myslel já, jen dokonale matematicky rozvedené.

[Jardax]

...

Tak to si musim nechat projit hlavou, takhle mi to nedava smysl...

[petrsida]

těžiště nemá s tíhovou silou mezi objekty nic společného, poloha těžiště je funkce hmotnosti a vzdálenosti, poloha libračního bodu je funkce hmotnosti a vzdálenosti na druhou, už z toho je to jasné

[lamid]

Dovolím si upozorniť, že gravitačná rovnováha a libračný bod sú dva rozdielne pojmy.

http://forum.kosmonautix.cz/viewtopic.p ... 020#p71720
"Ma to jeden háčik je to riešenie pre dva hmotné body bez pohybu ( alebo v rovnomernej rýchlosti).

Ak Mesiac obieha okolo Zeme, tak tam vstupuje odstredivá sila, ktorá drží Mesiac tam kde je a ktorá pôsobí aj na teleso, ktoré má byť v rovnováhe. A tak logicky musí byť bližšie k Zemi a sme u Lagrange-ovom riešení:
"

Gravitačná rovnováha je v bode kde sa gravitačné sily rovnajú. To je správne.
Ale libračný bod zahŕňa okrem gravitácie aj odstredivú silu, nakoľko dve telesa, ak sú blízko seba, tak sa musia obiehať, inak by sa pritiahli k sebe. Preto je libračný bod L1 bližšie k hmotnejšej planéte, ako bod gravitačnej rovnováhy.

[Alchymista]

vďaka,
tak toto je to, čo mi v úvahe unikalo - stále sa mi zdalo, že moja predstava je nejaká "neuplná", že mi tam ešte niečo chýba. Orbitálny pohyb.

edit: Ten vzorček - nie je aj vzorec pre určenie polomeru Hillovej sféry?
edit2: vlastne aj môže byť - libračné body L1a L2 ležia na hranici Hillovej sféry menšieho telesa

[lamid]

Libračný bod alebo Lagrangeov bod
http://forum.kosmonautix.cz/viewtopic.p ... 020#p71657

https://en.wikipedia.org/wiki/Lagrangian_point


Vrstevnice efektívneho potenciálu ( gravitačného a odstredivej sily) systému dvoch telies (Slnko a Zem). Šípky ukazujú smer potenciálu okolo Lagrange bodov – klesajúci smerom k nim (červená) alebo stúpajúci (modrá). L4 a L5 bod majú vysokú hodnotu potenciálu a sú stabilne. L1 L2 a L3 sú stabilné len v červenom smere, v modrom sú nestabilné.

Presnejší vypočet



Odvodenie vzťahu

je na holandskej wikipedii
https://nl.wikipedia.org/wiki/Lagrangepunt

Len poznámočka - ak sa podarí nájsť okrem týchto 5tych bodov ďalší, kde by sa mohol nachádzať vesmírny material, tak to je Nobelovu cenu.

[lamid]

Dám sem jeden obrázok, aj keď má prehodené označenie bodov L1 a L2

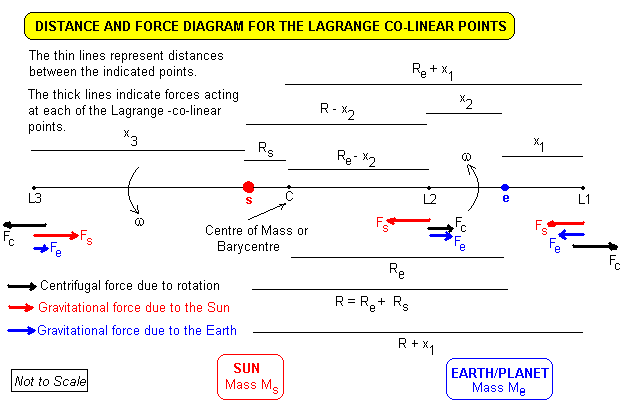
a link wolfram demo
http://demonstrations.wolfram.com/LagrangePoints/

Na obrázku
https://upload.wikimedia.org/wikipedia/ ... ential.jpg
je gradient vrstevníc silne prehnaný, v podstate je to hodne ploche, len teraz neviem nájsť vhodný 3D obrázok.


Pre predstavu stability L-bodov, pohyb asteroidov zviazaných s Jupiterom.

Pekne je vidieť, že L1 a L2 sú pre asteroidy "nezaujímavé", do L3 sú vystrčené ale utekajú z neho. Kde sa im páči to je L4 a L5, a ako sú rozťahané je vidieť ten plochý priebeh gradientu efektívneho potenciálu . Ak by bol priebeh strmý tak sú natlačené na seba v L4, L5 , asi by tam vznikla planéta?


Obrázky sú zo stránky Petr Scheirich
http://sajri.astronomy.cz/asteroidgroups/groups.htm

[lamid]

Ak má niekto záujem, tak funkcia použitá pre vykreslenie efektívneho potenciálu je


jej graf som si kedysi spravil:

pre parametre hodne vzdialene od hodnôt pre Slnko a Zem. q=0,1

[MaG]

A nedalo by se to prostě vysvětlit tak, že když se ocitnu v barycentru soustavy Pluto - Charon, tak logicky v tom místě jsem více přitahován Plutem a méně Charonem a proto to není totéž co librační bod? Pokud to říkám dobře, tak je to snad dostatečně srozumitelné i bez matematiky.