Gravitačný potencial - gravity potential
-
Sajri
- Zkušený vesmírný průzkumník
- Příspěvky: 381
- Reputace: 569
- Bydliště: Ondřejov
- Registrován: 21.3.2017 14:40
Re: Gravitačný potencial - gravity potential
Toho z navíc tady jsem si všimnul až teď. To tam opravdu být nemá ani ve 3D. Tím by totiž zmizela symetrie celého problému okolo roviny x-y, která tam ale být musí, protože v ní právě obíhají ta dvě hmotná tělesa.lamid píše:potom ale by malo byť U(x,y,z)=1/2(x^2+y^2+z^2)+(1-mu)/r1+mu/r2 ?
-
lamid
- Inženýr kosmonautiky

- Příspěvky: 1076
- Reputace: 0
- Registrován: 25.7.2013 0:22
- Kontaktovat uživatele:
Re: Gravitačný potencial - gravity potential
Áno, je to tak.
U(x,y,z)=(x^2+y^2)/2+(1-mu)/r1+mu/r2
nakoľko člen (x^2+y^2)/2 je vyjadrenie rotačnej energie ω hmotností m1 a m2.
a má rovnaký tvar ako v 2D
U(x,y)=(x^2+y^2)/2+(1-mu)/r1+mu/r2
kde pre
U(x,y)

a
U(x,y,z )


Stačilo pozorne prečítať hned prvý príspevok k Jacobi konštante, čo som sem dával, na predchádzajucej strane ktorý to rieši v 3D:

U(x,y,z)=(x^2+y^2)/2+(1-mu)/r1+mu/r2
nakoľko člen (x^2+y^2)/2 je vyjadrenie rotačnej energie ω hmotností m1 a m2.
a má rovnaký tvar ako v 2D
U(x,y)=(x^2+y^2)/2+(1-mu)/r1+mu/r2
kde pre
U(x,y)

a
U(x,y,z )


Stačilo pozorne prečítať hned prvý príspevok k Jacobi konštante, čo som sem dával, na predchádzajucej strane ktorý to rieši v 3D:

"Naše cnosti a naše vady sú neoddeliteľné ako sila a hmota, keď ich oddelíte človek prestane existovať."
Nikola Tesla
lamid58.blogspot.sk
Nikola Tesla
lamid58.blogspot.sk
-
lamid
- Inženýr kosmonautiky

- Příspěvky: 1076
- Reputace: 0
- Registrován: 25.7.2013 0:22
- Kontaktovat uživatele:
Re: Gravitačný potencial - gravity potential
Jacobi constant Cj=2* U(x,y,z) - v^2 :

Hranica dostupnej oblasti už jednoducho zrozumiteľná.
Hranice dosiahnuteľných oblastí navrstvené ako cibuľa:

S poklesom Cj (5.8, 3.7, 3.46, 3.1, 2.9 od stredu k okraju), ktoré je nepriamo úmerné zvýšeniu energie, sa zväčšuje dostupná oblasť.
P.S.
Poďakovanie Sajrimu za nasmerovanie.

Hranica dostupnej oblasti už jednoducho zrozumiteľná.
Hranice dosiahnuteľných oblastí navrstvené ako cibuľa:

S poklesom Cj (5.8, 3.7, 3.46, 3.1, 2.9 od stredu k okraju), ktoré je nepriamo úmerné zvýšeniu energie, sa zväčšuje dostupná oblasť.
P.S.
Poďakovanie Sajrimu za nasmerovanie.
Naposledy upravil(a) lamid dne 13.1.2019 9:29, celkem upraveno 2 x.
"Naše cnosti a naše vady sú neoddeliteľné ako sila a hmota, keď ich oddelíte človek prestane existovať."
Nikola Tesla
lamid58.blogspot.sk
Nikola Tesla
lamid58.blogspot.sk
-
lamid
- Inženýr kosmonautiky

- Příspěvky: 1076
- Reputace: 0
- Registrován: 25.7.2013 0:22
- Kontaktovat uživatele:
Re: Gravitačný potencial - gravity potential
Zväčšovanie, rast, dosiahnuteľných oblastí v 3D:
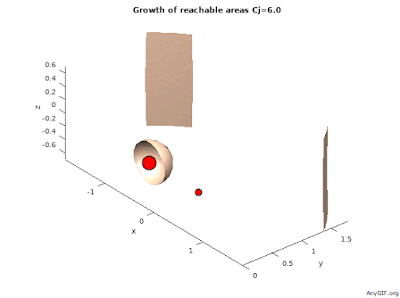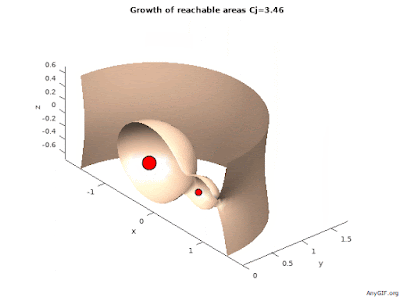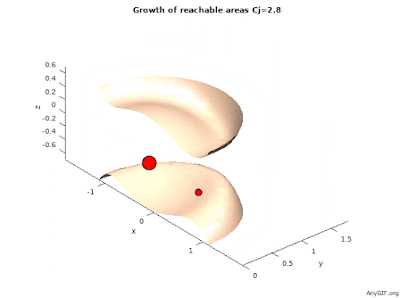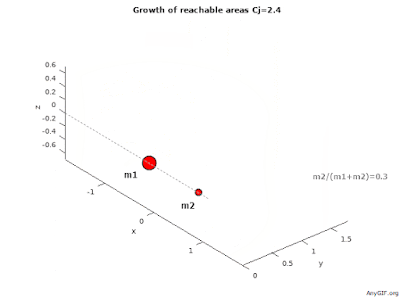
Hodnota Jacobi-ho konštanty tvorí plochu nulových rýchlostí/zero velocity surfaces/ čo je hranica dosiahnuteľnej oblasti.
Zväčšovanie dosiahnuteľných oblastí v 2D:

Hodnota Jacobi-ho konštanty tvorí krivku nulových rýchlostí/zero velocity curves/ čo je hranica dosiahnuteľnej oblasti.
Zaujímavosťou je dosiahnutie Lagrange-ových bodov L4 alebo L5 ako posledných, ak vystrelené teleso má energiu na ich dosiahnutie, tak dosiahne všade (v systéme obiehajúcich 2 hmotných bodov napr. Zem -Mesiac, Slnko-Jupiter a pod.) v rovine obehu hlavných telies m1, m2.
Let mimo rovinu x, y je stále obmedzený, a energeticky najnáročnejšie je let v smere osi Z.

Hodnota Jacobi-ho konštanty tvorí plochu nulových rýchlostí/zero velocity surfaces/ čo je hranica dosiahnuteľnej oblasti.
Zväčšovanie dosiahnuteľných oblastí v 2D:

Hodnota Jacobi-ho konštanty tvorí krivku nulových rýchlostí/zero velocity curves/ čo je hranica dosiahnuteľnej oblasti.
Zaujímavosťou je dosiahnutie Lagrange-ových bodov L4 alebo L5 ako posledných, ak vystrelené teleso má energiu na ich dosiahnutie, tak dosiahne všade (v systéme obiehajúcich 2 hmotných bodov napr. Zem -Mesiac, Slnko-Jupiter a pod.) v rovine obehu hlavných telies m1, m2.
Let mimo rovinu x, y je stále obmedzený, a energeticky najnáročnejšie je let v smere osi Z.
Naposledy upravil(a) lamid dne 13.1.2019 9:28, celkem upraveno 1 x.
"Naše cnosti a naše vady sú neoddeliteľné ako sila a hmota, keď ich oddelíte človek prestane existovať."
Nikola Tesla
lamid58.blogspot.sk
Nikola Tesla
lamid58.blogspot.sk
-
lamid
- Inženýr kosmonautiky

- Příspěvky: 1076
- Reputace: 0
- Registrován: 25.7.2013 0:22
- Kontaktovat uživatele:
Re: Gravitačný potencial - gravity potential
V poslednej animácii bol detail rastu dosiahnuteľných oblasti na osi "z" +-0,6.
Teraz troch širší pohlaď:

Teraz troch širší pohlaď:

Naposledy upravil(a) lamid dne 13.1.2019 9:27, celkem upraveno 1 x.
"Naše cnosti a naše vady sú neoddeliteľné ako sila a hmota, keď ich oddelíte človek prestane existovať."
Nikola Tesla
lamid58.blogspot.sk
Nikola Tesla
lamid58.blogspot.sk
-
lamid
- Inženýr kosmonautiky

- Příspěvky: 1076
- Reputace: 0
- Registrován: 25.7.2013 0:22
- Kontaktovat uživatele:
Re: Gravitačný potencial - gravity potential
Naposledy upravil(a) lamid dne 13.1.2019 9:24, celkem upraveno 1 x.
"Naše cnosti a naše vady sú neoddeliteľné ako sila a hmota, keď ich oddelíte človek prestane existovať."
Nikola Tesla
lamid58.blogspot.sk
Nikola Tesla
lamid58.blogspot.sk
-
lamid
- Inženýr kosmonautiky

- Příspěvky: 1076
- Reputace: 0
- Registrován: 25.7.2013 0:22
- Kontaktovat uživatele:
Re: Gravitačný potencial - gravity potential
Ako v jednom grafe Jacobi-ho integrálu
jednoducho zobraziť
plochy a krivky nulovej rýchlosti

rezom v z=0
pohlaď na krivky nulovej rýchlosti/zero velicity curves obrázku uvedenom vyššie v rovine x-y z=0 :

jednoducho zobraziť
plochy a krivky nulovej rýchlosti

rezom v z=0
pohlaď na krivky nulovej rýchlosti/zero velicity curves obrázku uvedenom vyššie v rovine x-y z=0 :

Naposledy upravil(a) lamid dne 13.1.2019 9:25, celkem upraveno 2 x.
"Naše cnosti a naše vady sú neoddeliteľné ako sila a hmota, keď ich oddelíte človek prestane existovať."
Nikola Tesla
lamid58.blogspot.sk
Nikola Tesla
lamid58.blogspot.sk
-
lamid
- Inženýr kosmonautiky

- Příspěvky: 1076
- Reputace: 0
- Registrován: 25.7.2013 0:22
- Kontaktovat uživatele:
Re: Gravitačný potencial - gravity potential
Lepšie ako 100x počuť je 1x vidieť:
Šedá oblasť je zakázaná oblasť. Teleso nemôže vstúpiť do tejto plochy.
Nájdením Jacobi obrysu povrchu/krivky zodpovedajúceho nulovej rýchlosti môžeme nájsť oblasti, kde teleso m3 nemôže ísť - zakázané oblasti.
Video je zobrazené sidericky (m1 a m2 rotujú) (pozorovateľ je mimo sústavu).
Alternatívnym zobrazením je synodické. V ňom zostávajú rotujúce telesa m1 a m2 zobrazene stacionárne a teleso m3 sa pohybuje okolo nich (pozorovateľ je vo vnútry sústavy).
https://youtu.be/4ACSw2IRTfM
Šedá oblasť je zakázaná oblasť. Teleso nemôže vstúpiť do tejto plochy.
Nájdením Jacobi obrysu povrchu/krivky zodpovedajúceho nulovej rýchlosti môžeme nájsť oblasti, kde teleso m3 nemôže ísť - zakázané oblasti.
Video je zobrazené sidericky (m1 a m2 rotujú) (pozorovateľ je mimo sústavu).
Alternatívnym zobrazením je synodické. V ňom zostávajú rotujúce telesa m1 a m2 zobrazene stacionárne a teleso m3 sa pohybuje okolo nich (pozorovateľ je vo vnútry sústavy).
https://youtu.be/4ACSw2IRTfM
"Naše cnosti a naše vady sú neoddeliteľné ako sila a hmota, keď ich oddelíte človek prestane existovať."
Nikola Tesla
lamid58.blogspot.sk
Nikola Tesla
lamid58.blogspot.sk
-
lamid
- Inženýr kosmonautiky

- Příspěvky: 1076
- Reputace: 0
- Registrován: 25.7.2013 0:22
- Kontaktovat uživatele:
Re: Gravitačný potencial - gravity potential
"Naše cnosti a naše vady sú neoddeliteľné ako sila a hmota, keď ich oddelíte človek prestane existovať."
Nikola Tesla
lamid58.blogspot.sk
Nikola Tesla
lamid58.blogspot.sk

